|
|
|
|
|
§ 2. Параллелограмм и трапеция Задачи к § 2. Параллелограмм и трапеция (продолжение)385. Докажите теорему Фалеса1: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. 1 Фалес Милетский — древнегреческий учёный (ок. 625—547 гг. до н. э.). Решение Пусть на прямой l1 отложены равные отрезки А1А2, А2А3, А3А4, ... и через их концы проведены параллельные прямые, которые пересекают прямую l2 в точках В1, В2, В3, В4, ... (рис. 165). Требуется доказать, что отрезки В1В2, В2В3, В3В4, ... равны друг другу. Докажем, например, что В1В2 = В2В3. Рассмотрим сначала случай, когда прямые l1, и l2 параллельны (рис. 165, а). Тогда A1А2 = В1В2 и А2А3 = В2В3 как противоположные стороны параллелограммов А1В1В2А2 и А2В2В3А3. Так как А1А2 = А2А3, то и В1В2 = В2В3. Если прямые l1 и l2 не параллельны, то через точку В1 проведём прямую l, параллельную прямой l1 (рис. 165, б). Она пересечёт прямые А2В2 и А3В3 в некоторых точках С и D. Так как А1А2 = А2А3, то по доказанному B1C = CB. Отсюда получаем: B1B2 = B1B3 (задача 384). Аналогично можно доказать, что В2В3 = В3В4 и т. д.
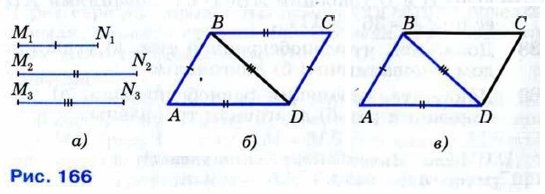
386. Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции. 387. Найдите углы В и В трапеции ABCD с основаниями AD и ВС, если ∠A = 36°, ∠C =117°. 388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равны; б) диагонали равны. 389. Докажите, что трапеция равнобедренная, если: а) углы при основании равны; б) диагонали трапеции равны. 390. Один из углов равнобедренной трапеции равен 68°. Найдите остальные углы трапеции. 391. Докажите, что из одинаковых плиток, имеющих форму равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть плоскости. 392. 393. Решение в) Даны три отрезка M1N1, M2N2, M3N3 (рис. 166, а). Требуется построить параллелограмм ABCD, у которого смежные стороны, скажем АВ и AD, равны соответственно отрезкам M1N1 и M2N2, а диагональ BD равна отрезку M3N3. Проведём решение задачи по схеме, описанной на с. 94. Анализ Допустим, что искомый параллелограмм ABCD построен (рис. 166, б). Мы видим, что стороны треугольника ABD равны данным отрезкам M1N1, M2N2 и M3N3. Это обстоятельство подсказывает следующий путь решения задачи: сначала нужно построить по трём сторонам треугольник ABD, а затем достроить его до параллелограмма ABCD. Построение Строим треугольник ABD так, чтобы его стороны АВ, AD и BD равнялись соответственно отрезкам M2N2 и M3N3 (как это сделать, мы знаем из курса 7 класса). Затем построим прямую, проходящую через точку В параллельно AD, и вторую прямую, проходящую через точку D параллельно АВ (как это сделать, мы также знаем из курса 7 класса). Точку пересечения этих прямых обозначим буквой С (рис. 166, в). Четырёхугольник ABCD и есть искомый параллелограмм.
Доказательство По построению АВ || CD и ВС || AD, поэтому ABCD — параллелограмм. Смежные стороны параллелограмма ABCD по построению равны отрезкам и M2N2, а диагональ BD равна отрезку M3N3, т. е. параллелограмм ABCD — искомый. Исследование Ясно, что если по трём данным отрезкам M1N1, M2N2 и M3N3 можно построить треугольник ABD, стороны которого равны этим отрезкам, то можно построить и параллелограмм ABCD. Но треугольник ABD можно построить не всегда. Если какой-то из трёх данных отрезков больше или равен сумме двух других, то треугольник ABD, а значит, и параллелограмм ABCD построить нельзя. Попробуйте самостоятельно доказать, что если задача имеет решение, то это решение единственно (см. п. 39).
|
|
|




 Основания прямоугольной трапеции равны а и b, один из углов равен α. Найдите: а) большую боковую сторону трапеции, если а = 4см, b = 7см, α = 60°; б) меньшую боковую сторону трапеции, если а = 10 см, b = 15 см, α = 45°.
Основания прямоугольной трапеции равны а и b, один из углов равен α. Найдите: а) большую боковую сторону трапеции, если а = 4см, b = 7см, α = 60°; б) меньшую боковую сторону трапеции, если а = 10 см, b = 15 см, α = 45°.